
Cargas Distribuidas
En algunos textos las denominan: Cargas repartidas o cargas no puntuales, generalmente no se analizan ya que sus efectos en las estructuras son menores que las cargas puntuales.
Se considera una carga distribuida a todo material o elemento que es soportado por una viga, ya sea a modo permanente dentro de la estructura como: la placa de un techo, el viento, presión hidrostática, etc.; o accidental como: nieve, agua, depósitos de materiales, etc.
Incluir las cargas distribuidas dentro del análisis de las estructuras logra evitar las grietas en las zonas de las vigas, ocasionado por una mayor tensión del cual no pueden soportar.
Ejemplos:


Cargas distribuidas más comunes:
Cargas distribuidas rectangulares:
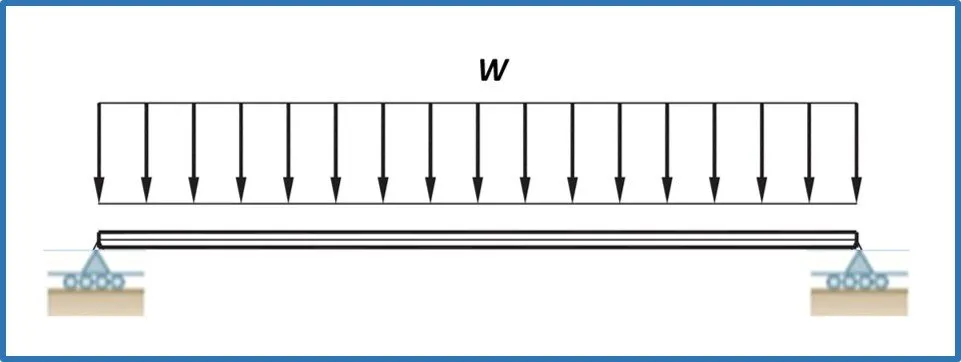
Cargas distribuidas triangulares
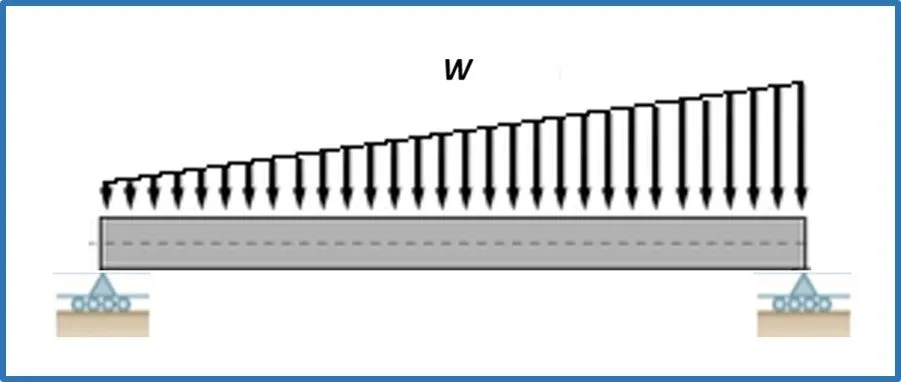
Cargas distribuidas combinadas
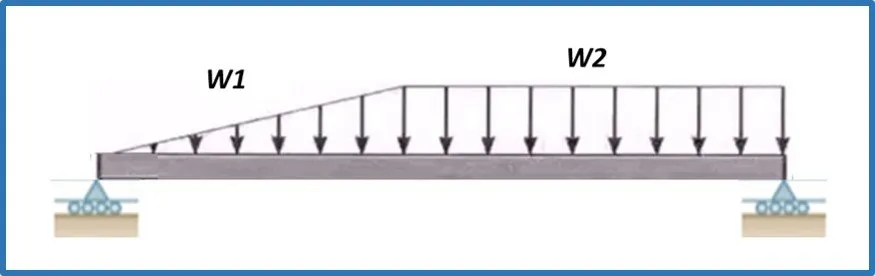

Transformando de cargas distribuidas a cargas puntuales:
Cargas distribuida rectangular a carga puntual:
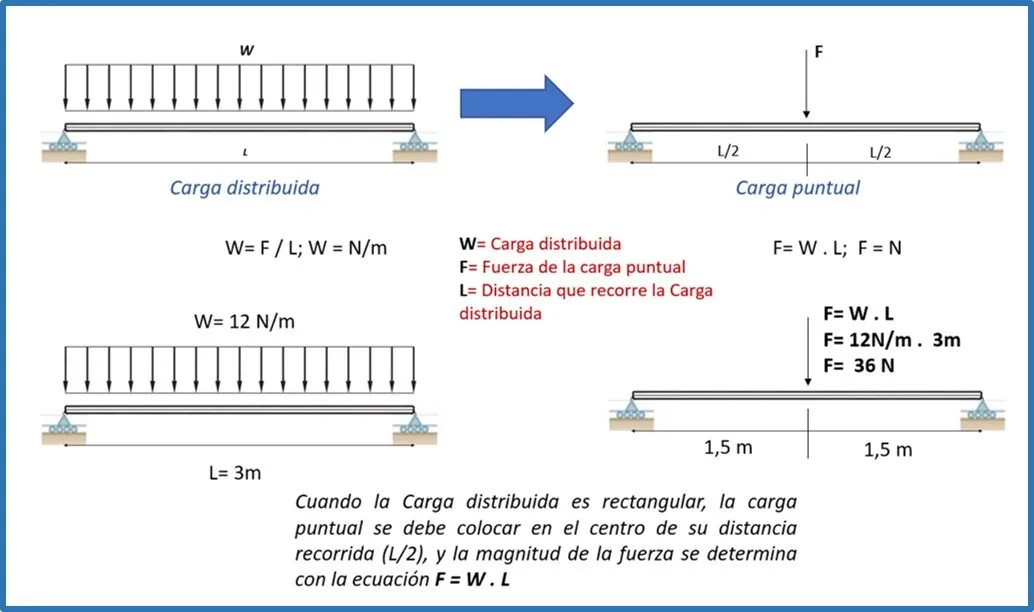
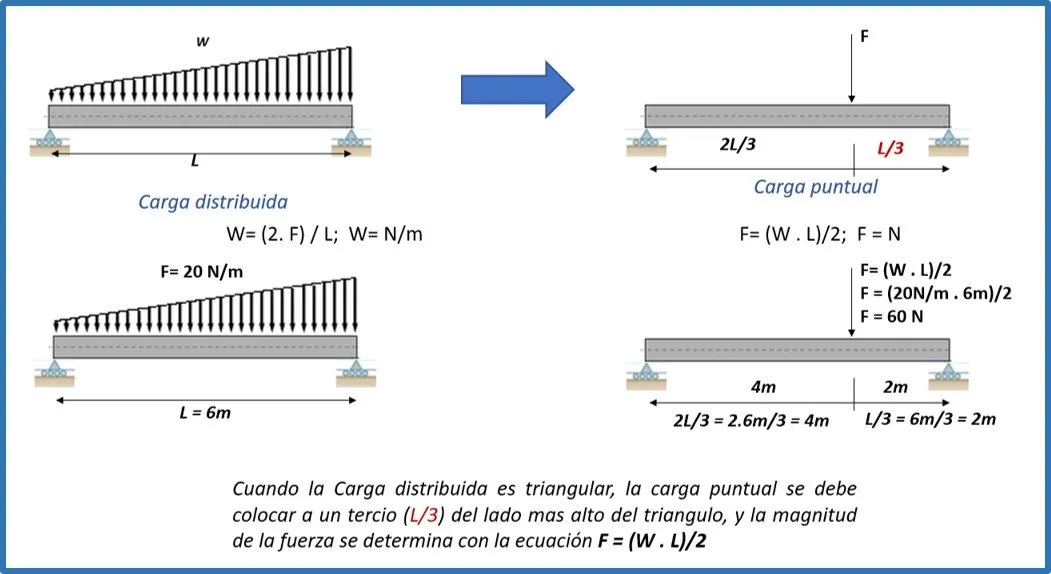
Cargas distribuida triangular a carga puntual:

Reacciones de los apoyos con cargas distribuidas:
Procedimiento:
- Detectar que tipo de carga o cargas distribuidas tiene la estructura.
- Convertir a carga puntual cada carga distribuida, atento a la forma y a la distancia que recorre la carga distribuida.
- Si la carga distribuida es rectangular, la magnitud de la carga puntual es: F = W.d, y la carga puntual debe colocarse en el centro o punto medio de la distancia de la carga distribuida.
- Si la carga distribuida es de forma triangular, la magnitud de la carga puntual es: F = (W.d)/2, mientras que la ubicación de la carga puntual debe ser a un tercio del lado más alto del triángulo (L/3)
- Una vez determinadas las cargas puntuales, se deben graficar las reacciones de los apoyos, tomando en cuenta si son de las que generan una o dos reacciones, generalmente las graficamos con sentido positivo.
- Obtenido el diagrama de cuerpo libre, identificamos las incógnitas y seleccionamos algún punto de los apoyos para calcular el momento (la que tenga más incógnitas), en condiciones de equilibrio, ΣMo = 0.
- Y utilizando el resto de las ecuaciones en condiciones de equilibro se determinan las reacciones faltantes, ΣFx = 0, ΣFy = 0.
- Si al determinar alguna de las reacciones da resultado con signo negativo, quiere decir que el sentido propuesto en el primer diagrama de cuerpo libre es errado, basta con graficar nuevamente con los sentidos corregidos.

Ejemplo 1:
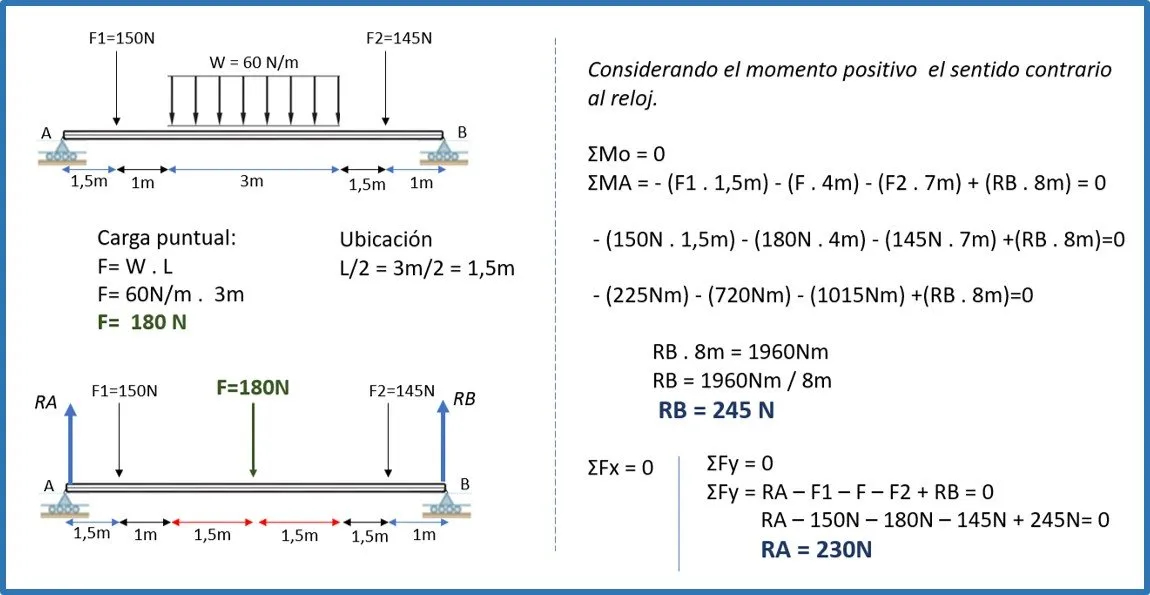
Ejemplo 2:
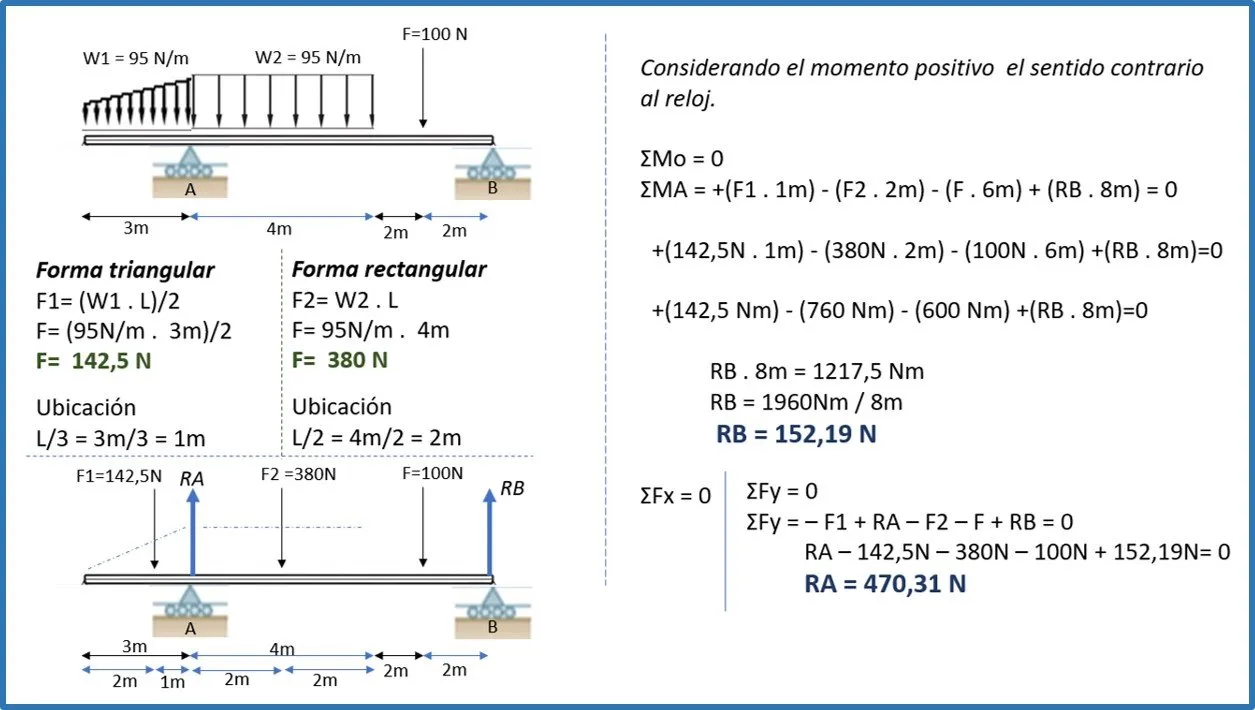
Observación en el ejemplo 2:
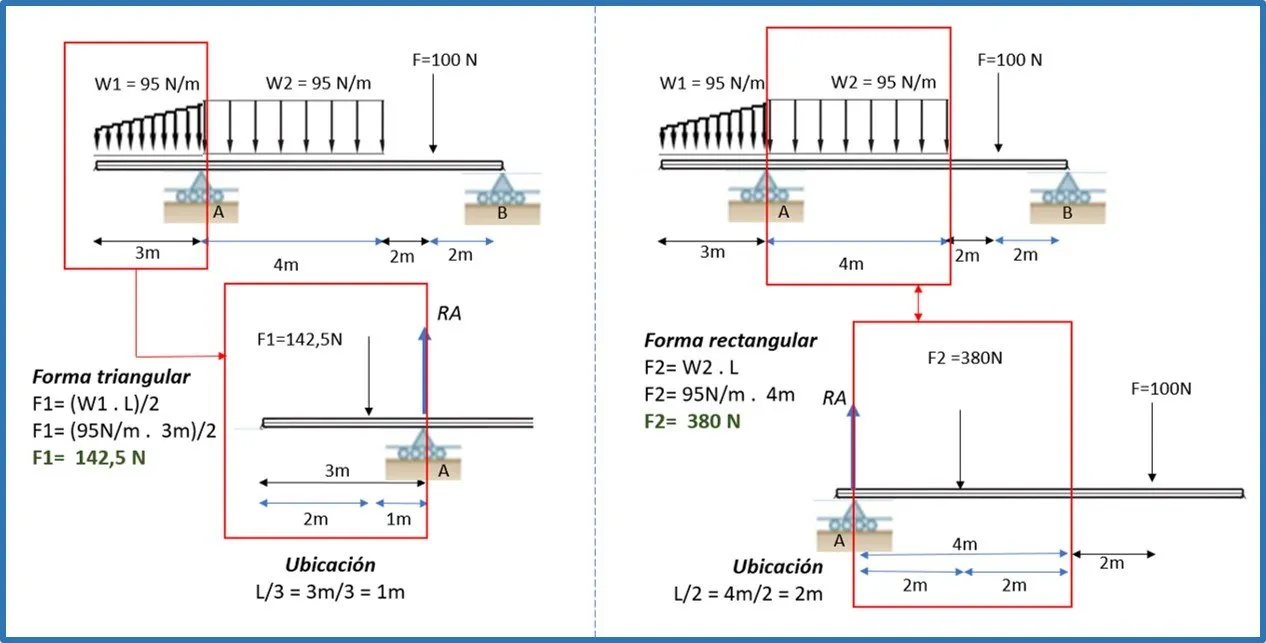

Temas anteriores:
- Bienvenidos a: Mecánica Aplicada
- Orígenes y Aplicaciones de la Mecánica Aplicada
- Fuerza resultante de un Sistema de Fuerzas.
- Paso a paso para determinar el momento de una fuerza.
- Determinando las Reacciones de los apoyos
- Recursos didácticos para estudiar Mecánica Aplicada Online.

Bibliografía:
Budynas, Richard G. (2008) Diseño en ingeniería mecánica, Editorial McGraw-Hill Interamericana.
Meriam, J.L y Kraige L.G. (2008) Mecánica par ingenieros, Editorial Reveré, S.A..
Beer, Johnston y Cornwell. (2010) Mecánica vectorial para ingeniaros, Dinámica, Editorial McGraw-Hill Interamericana, Novena edición.
Beer, Johnston y Cornwell. (2010) Mecánica vectorial para ingeniaros, Estática, Editorial McGraw-Hill Interamericana, Novena edición.

Realizado por:
Ing. Alcides Cádiz
Investigador y Generador de Contenido
Posdata: Las imágenes usadas para este blog fueron creadas por el propio autor o tomadas de: https://pixabay.com/es/ (repositorio de imágenes sin derecho de autor): 12.1 2.2 2.3

