
Reacciones de los apoyos:

Conceptos físicos a utilizar para determinar las reacciones de los apoyos:
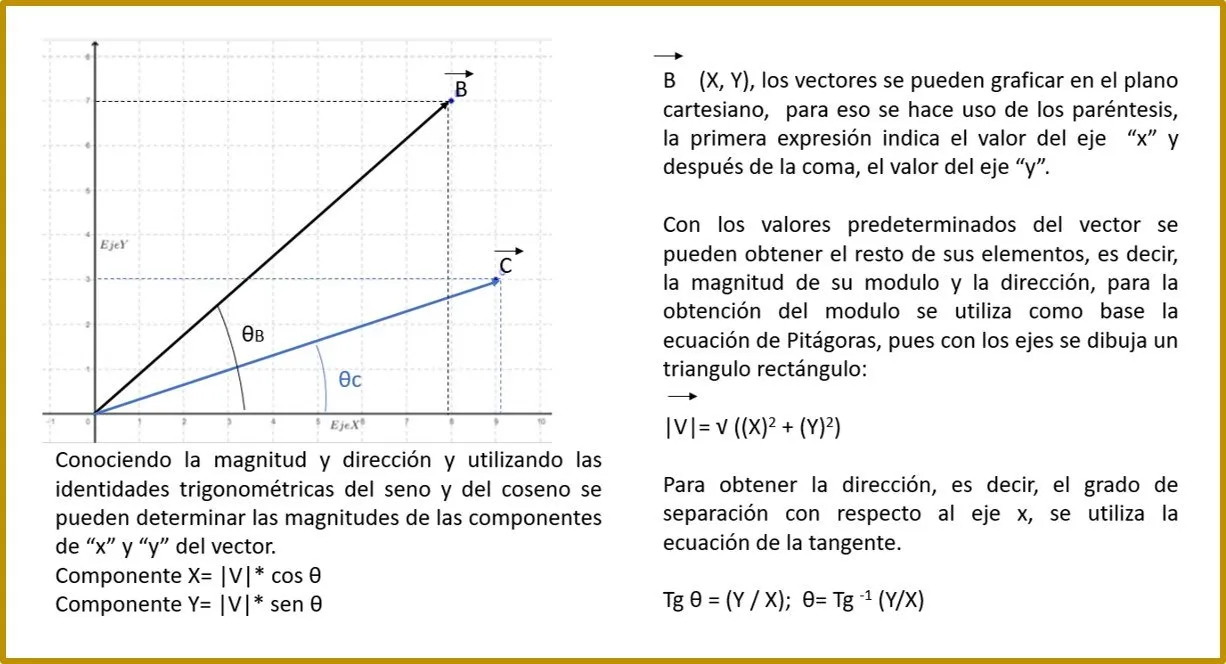
- La teoría de los vectores es aplicada para las fuerzas, con ellas se puede determinar el modulo o magnitud, el sentido, la dirección y las componentes:
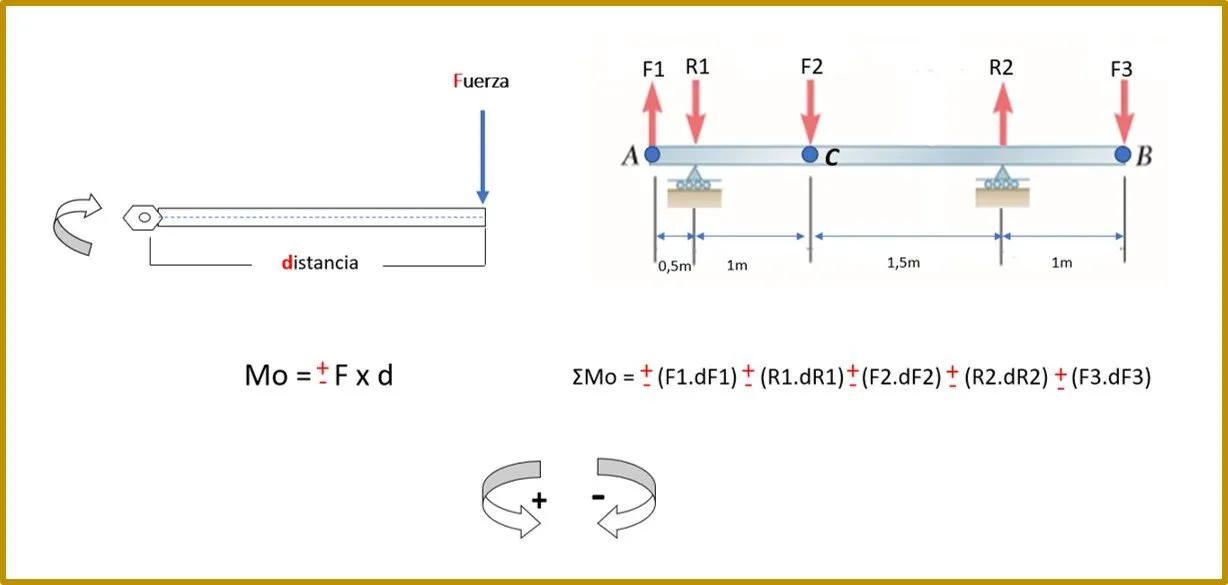
- El momento de una fuerza permite determinar el efecto rotacional que puede provocar una fuerza a una estructura, ya sea una sola o un grupo de fuerzas.

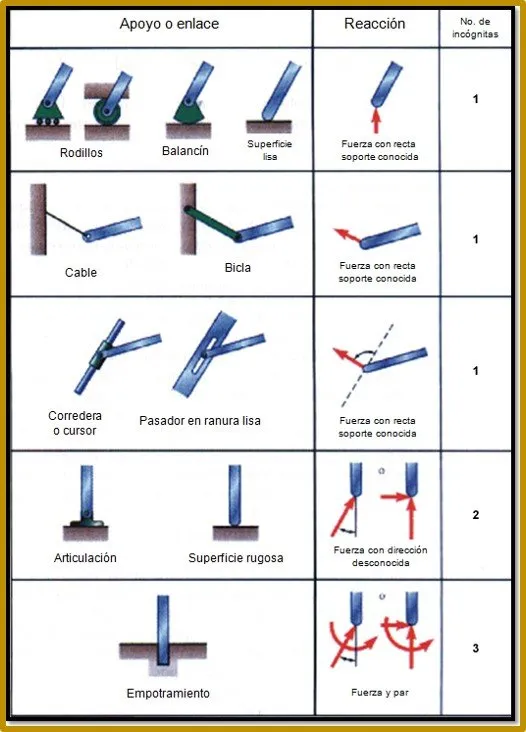
Tipos de apoyos:
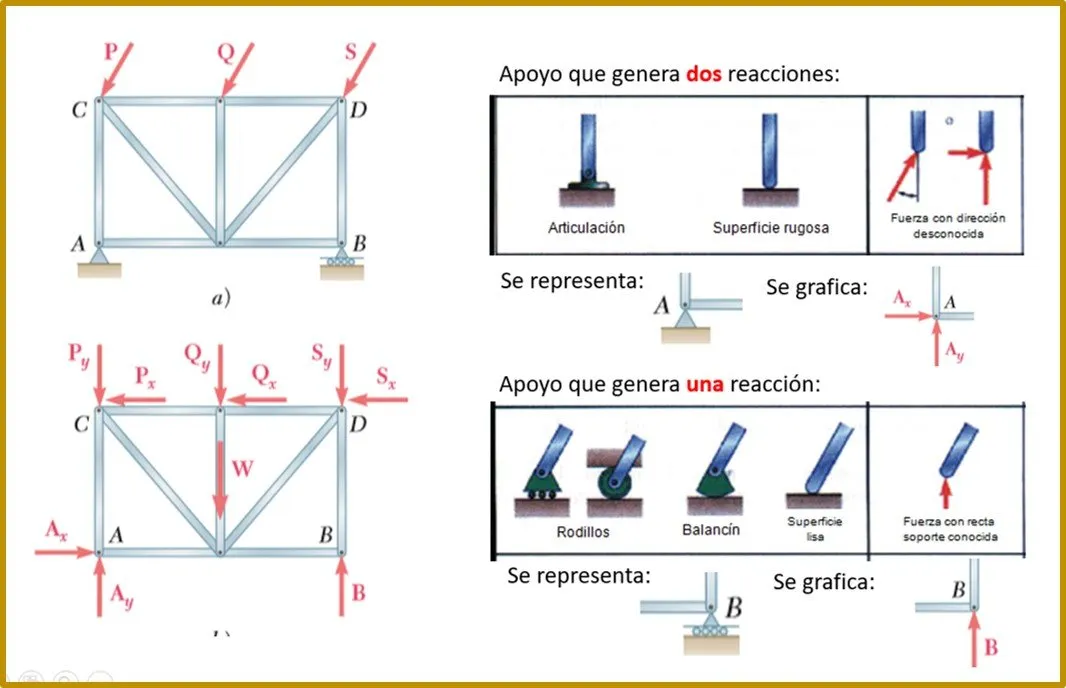

Pasos para calcular las reacciones de los apoyos:
Graficar las reacciones de los apoyos, depende del tipo de apoyo se grafica una o dos reacciones, la dirección a indicar es temporal, generalmente se tiende a colocar direcciones positivas, pero si al realizar el calculo la magnitud de la reacción el valor es negativo, eso indica que la dirección indicada es contraria de la planteada inicialmente.
Seleccionar un punto para determinar la sumatoria del momento, si los apoyos son del tipo que genera una sola reacción, el punto a escoger para realizar el primer momento puede ser cualquiera de donde están ubicados los apoyos.
Verificar que las fuerzas estén perpendiculares al punto seleccionado para la aplicación del momento, de no ser así, se deben descomponer en x e y respectivamente.
Recordemos que estamos trabajando bajo la premisa de condiciones de equilibrio, por lo tanto, la sumatoria del momento es nula, igualamos a cero, lo que nos genera una ecuación con una incógnita (la reacción del apoyo) que podemos despejar.
Utilizando las otras ecuaciones de equilibrio (ΣFx = 0 y ΣFy = 0) determinamos la o las reacciones faltantes.
Si al plantear las ecuaciones nos generan ecuaciones con dos incógnitas, podemos utilizar estrategias matemáticas (sistemas de ecuaciones con dos incógnitas: igualación, reducción y sustitución)
Graficar la estructura con los sentidos de las reacciones de los apoyos confirmadas.

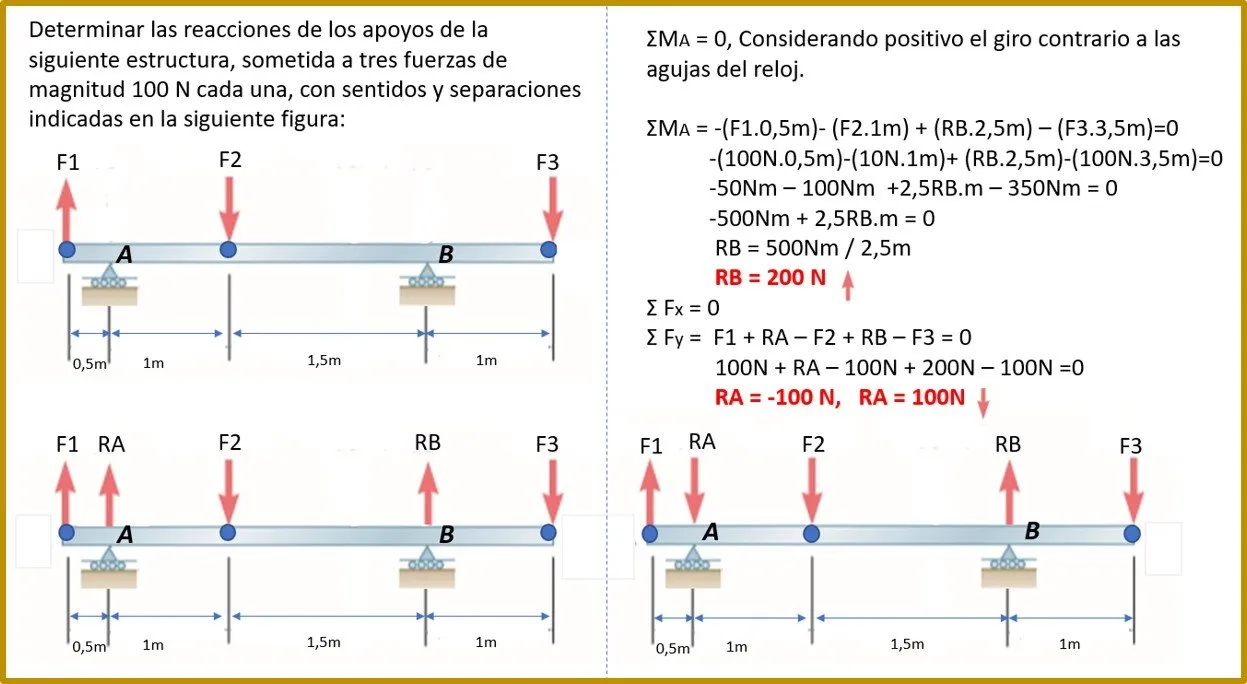
Ejemplo 1:
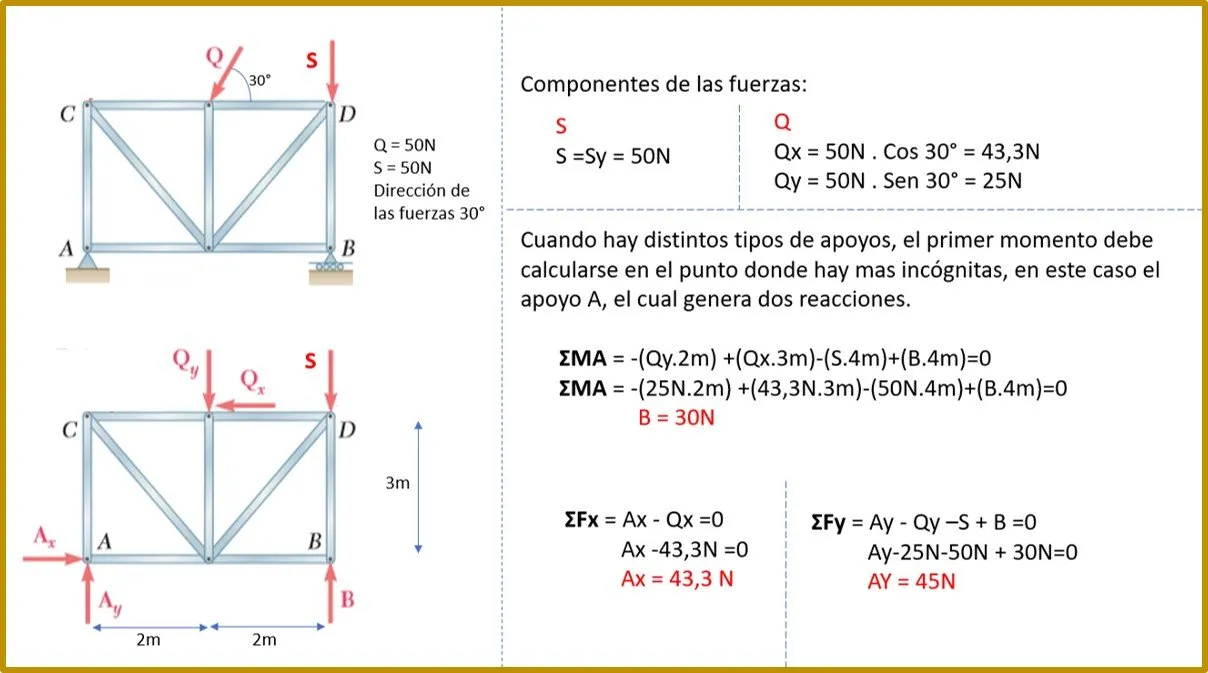
Ejemplo 2:

Conclusiones:
En el ejemplo 1, las fuerzas: F1, F2 y F3 son fuerzas que pertenecen al eje "y" por tal razón no es necesario determinar sus componentes, mientras que en el ejemplo 2 la fuerza Q está inclinada, por lo tanto se debió calcular sus componentes en "x" y "y".
En el ejemplo 1 sus apoyos son representados como rodillos o balancines por lo tanto se le gráfico una sola reacción por apoyo, en el ejemplo 2 los apoyos son distintos, el apoyo A es del tipo articulado, por esa razón se le gráfico dos reacciones.
Al utilizar la ΣFy = 0 en el ejemplo 1, y despejar la reacción incógnita observamos que su magnitud da negativo, cuando eso ocurre quiere decir que el sentido de la reacción es contraria a la inicial, recordemos que los sentidos que les graficamos a las reacciones son temporales, si el resultado es positivo confirma que ese sentido es el correcto, sino, en la gráfica corregimos el sentido y para cálculos posteriores se toma en cuenta el cambio encontrado.
En el ejemplo 1 la sumatoria del momento también pudo haberse realizado con referencia al punto B, y se hubieran obtenido los mismos resultados (puedes probarlo), sin embargo, en el ejemplo 2 hay apoyos distintos, y en esos casos el punto de referencia obligatorio y esencial para efectuar el momento es el apoyo que genera mas reacciones.

Temas anteriores:
- Bienvenidos a: Mecánica Aplicada (24/05/2018)
- Orígenes y Aplicaciones de la Mecánica Aplicada (31/05/2018)
- Fuerza resultante de un Sistema de Fuerzas, Mecánica Aplicada. (07/06/2018)
- Paso a paso para determinar el momento de una fuerza, Mecánica Aplicada. (14/06/2018)

Bibliografía:
Budynas, Richard G. (2008) Diseño en ingeniería mecánica, Editorial McGraw-Hill Interamericana.
Meriam, J.L y Kraige L.G. (2008) Mecánica par ingenieros, Editorial Reveré, S.A..
Beer, Johnston y Cornwell. (2010) Mecánica vectorial para ingeniaros, Dinámica, Editorial McGraw-Hill Interamericana, Novena edición.
Beer, Johnston y Cornwell. (2010) Mecánica vectorial para ingeniaros, Estática, Editorial McGraw-Hill Interamericana, Novena edición.

Ing. Alcides Cádiz #Venezuela
Posdata: Las imágenes usadas para este y los siguientes blogs de esta serie de Mecánica Aplicada son de elaboración propia o tomadas de: https://pixabay.com/es/ (repositorio de imágenes sin derecho de autor)
